Биноминальное распределение. Биномиальный закон распределения
Конечно, при вычислении кумулятивной функции распределения следует воспользоваться упомянутой связью биномиального и бета- распределения. Этот способ заведомо лучше непосредственного суммирования, когда n > 10.
В классических учебниках по статистике для получения значений биномиального распределения часто рекомендуют использовать формулы, основанные на предельных теоремах (типа формулы Муавра-Лапласа). Необходимо отметить, что с чисто вычислительной точки зрения ценность этих теорем близка к нулю, особенно сейчас, когда практически на каждом столе стоит мощный компьютер. Основной недостаток приведенных аппроксимаций – их совершенно недостаточная точность при значениях n, характерных для большинства приложений. Не меньшим недостатком является и отсутствие сколько-нибудь четких рекомендаций о применимости той или иной аппроксимации (в стандартных текстах приводятся лишь асимптотические формулировки, они не сопровождаются оценками точности и, следовательно, мало полезны). Я бы сказал, что обе формулы пригодны лишь при n < 200 и для совсем грубых, ориентировочных расчетов, причем делаемых “вручную” с помощью статистических таблиц. А вот связь между биномиальным распределением и бета-распределением позволяет вычислять биномиальное распределение достаточно экономно.
Я не рассматриваю здесь задачу поиска квантилей: для дискретных распределений она тривиальна, а в тех задачах, где такие распределения возникают, она, как правило, и не актуальна. Если же квантили все-таки понадобятся, рекомендую так переформулировать задачу, чтобы работать с p-значениями (наблюденными значимостями). Вот пример: при реализации некоторых переборных алгоритмов на каждом шаге требуется проверять статистическую гипотезу о биномиальной случайной величине. Согласно классическому подходу на каждом шаге нужно вычислить статистику критерия и сравнить ее значение с границей критического множества. Поскольку, однако, алгоритм переборный, приходится определять границу критического множества каждый раз заново (ведь от шага к шагу объем выборки меняется), что непроизводительно увеличивает временные затраты. Современный подход рекомендует вычислять наблюденную значимость и сравнивать ее с доверительной вероятностью, экономя на поиске квантилей.
Поэтому в приводимых ниже кодах отсутствует вычисление обратной функции, взамен приведена функция rev_binomialDF , которая вычисляет вероятность p успеха в отдельном испытании по заданному количеству n испытаний, числу m успехов в них и значению y вероятности получить эти m успехов. При этом используется вышеупомянутая связь между биномиальным и бета распределениями.
Фактически, эта функция позволяет получать границы доверительных интервалов.
В самом деле, предположим, что в n
биномиальных испытаниях мы получили m
успехов. Как известно, левая граница двухстороннего доверительного интервала
для параметра p с доверительным уровнем
равна 0, если
m = 0, а для
является решением уравнения  .
Аналогично, правая граница равна 1,
если m = n, а для
является решением уравнения
.
Аналогично, правая граница равна 1,
если m = n, а для
является решением уравнения  .
Отсюда вытекает, что для поиска левой границы мы должны решать относительно
уравнение
.
Отсюда вытекает, что для поиска левой границы мы должны решать относительно
уравнение
 ,
а для поиска правой – уравнение
,
а для поиска правой – уравнение
 .
Они и решаются в функциях binom_leftCI и binom_rightCI ,
возвращающих верхнюю и нижнюю границы двустороннего доверительного интервала
соответственно.
.
Они и решаются в функциях binom_leftCI и binom_rightCI ,
возвращающих верхнюю и нижнюю границы двустороннего доверительного интервала
соответственно.
Хочу заметить, что если не нужна совсем уж неимоверная точность, то
при достаточно больших n можно воспользоваться
следующей аппроксимацией [Б.Л. ван дер Варден, Математическая статистика.
М: ИЛ, 1960, гл. 2, разд. 7]:
 ,
где g – квантиль нормального распределения.
Ценность этой аппроксимации в том, что имеются очень простые приближения,
позволяющие вычислять квантили нормального распределения (см. текст о вычислении
нормального распределения и соответствующий раздел данного справочника).
В моей практике (в основном, при n > 100) эта аппроксимация давала примерно 3-4 знака, чего, как правило,
вполне достаточно.
,
где g – квантиль нормального распределения.
Ценность этой аппроксимации в том, что имеются очень простые приближения,
позволяющие вычислять квантили нормального распределения (см. текст о вычислении
нормального распределения и соответствующий раздел данного справочника).
В моей практике (в основном, при n > 100) эта аппроксимация давала примерно 3-4 знака, чего, как правило,
вполне достаточно.
Для вычислений с помощью нижеследующих кодов потребуются файлы betaDF.h , betaDF.cpp (см. раздел о бета-распределении), а также logGamma.h , logGamma.cpp (см. приложение А). Вы можете посмотреть также пример использования функций.
Файл binomialDF.h
| #ifndef __BINOMIAL_H__ #include "betaDF.h" double binomialDF(double trials, double successes, double p); /* * Пусть имеется "trials" независимых наблюдений * с вероятностью "p" успеха в каждом. * Вычисляется вероятность B(successes|trials,p) того, что число * успехов заключено между 0 и "successes" (включительно). */ double rev_binomialDF(double trials, double successes, double y); /* * Пусть известна вероятность y наступления не менее m успехов * в trials испытаниях схемы Бернулли. Функция находит вероятность p * успеха в отдельном испытании. * * В вычислениях используется следующее соотношение * * 1 - p = rev_Beta(trials-successes| successes+1, y). */ double binom_leftCI(double trials, double successes, double level); /* Пусть имеется "trials" независимых наблюдений * с вероятностью "p" успеха в каждом * и количество успехов равно "successes". * Вычисляется левая граница двустороннего доверительного интервала * с уровнем значимости level. */ double binom_rightCI(double n, double successes, double level); /* Пусть имеется "trials" независимых наблюдений * с вероятностью "p" успеха в каждом * и количество успехов равно "successes". * Вычисляется правая граница двустороннего доверительного интервала * с уровнем значимости level. */ #endif /* Ends #ifndef __BINOMIAL_H__ */ |
Файл binomialDF.cpp
|
/***********************************************************/
/* Биномиальное распределение */
/***********************************************************/
#include |
Можно выделить наиболее часто встречающиеся законы распределения дискретных случайных величин:
- Биномиальный закон распределения
- Пуассоновский закон распределения
- Геометрический закон распределения
- Гипергеометрический закон распределения
Для данных распределений дискретных случайных величин расчет вероятностей их значений, а также числовых характеристик (математическое ожидание, дисперсия, и т.д.) производится по определенных «формулам». Поэтому очень важно знать данные типы распределений и их основные свойства.
1. Биномиальный закон распределения.
Дискретная случайная величина $X$ подчинена биномиальному закону распределения вероятностей, если она принимает значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=C^k_n\cdot p^k\cdot {\left(1-p\right)}^{n-k}$. Фактически, случайная величина $X$ - это число появлений события $A$ в $n$ независимых испытаний . Закон распределения вероятностей случайной величины $X$:
$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & \dots & n \\
\hline
p_i & P_n\left(0\right) & P_n\left(1\right) & \dots & P_n\left(n\right) \\
\hline
\end{array}$
Для такой случайной величины математическое ожидание $M\left(X\right)=np$, дисперсия $D\left(X\right)=np\left(1-p\right)$.
Пример . В семье двое детей. Считая вероятности рождения мальчика и девочки равными $0,5$, найти закон распределения случайной величины $\xi $ - числа мальчиков в семье.
Пусть случайная величина $\xi $ - число мальчиков в семье. Значения, которые может принимать $\xi:\ 0,\ 1,\ 2$. Вероятности этих значений можно найти по формуле $P\left(\xi =k\right)=C^k_n\cdot p^k\cdot {\left(1-p\right)}^{n-k}$, где $n=2$ - число независимых испытаний, $p=0,5$ - вероятность появления события в серии из $n$ испытаний. Получаем:
$P\left(\xi =0\right)=C^0_2\cdot {0,5}^0\cdot {\left(1-0,5\right)}^{2-0}={0,5}^2=0,25;$
$P\left(\xi =1\right)=C^1_2\cdot 0,5\cdot {\left(1-0,5\right)}^{2-1}=2\cdot 0,5\cdot 0,5=0,5;$
$P\left(\xi =2\right)=C^2_2\cdot {0,5}^2\cdot {\left(1-0,5\right)}^{2-2}={0,5}^2=0,25.$
Тогда закон распределения случайной величины $\xi $ есть соответствие между значениями $0,\ 1,\ 2$ и их вероятностями, то есть:
$\begin{array}{|c|c|}
\hline
\xi & 0 & 1 & 2 \\
\hline
P(\xi) & 0,25 & 0,5 & 0,25 \\
\hline
\end{array}$
Сумма вероятностей в законе распределения должна быть равна $1$, то есть $\sum _{i=1}^{n}P(\xi _{{\rm i}})=0,25+0,5+0,25=1 $.
Математическое ожидание $M\left(\xi \right)=np=2\cdot 0,5=1$, дисперсия $D\left(\xi \right)=np\left(1-p\right)=2\cdot 0,5\cdot 0,5=0,5$, среднее квадратическое отклонение $\sigma \left(\xi \right)=\sqrt{D\left(\xi \right)}=\sqrt{0,5}\approx 0,707$.
2. Закон распределения Пуассона.
Если дискретная случайная величина $X$ может принимать только целые неотрицательные значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$, то говорят, что она подчинена закону распределения Пуассона с параметром $\lambda $. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda $.
Замечание . Особенность этого распределения заключается в том, что мы на основании опытных данных находим оценки $M\left(X\right),\ D\left(X\right)$, если полученные оценки близки между собой, то у нас есть основание утверждать, что случайная величина подчинена закону распределения Пуассона.
Пример . Примерами случайных величин, подчиненных закону распределения Пуассона, могут быть: число автомашин, которые будут обслужены завтра автозаправочной станцией; число бракованных изделий в произведенной продукции.
Пример . Завод отправил на базу $500$ изделий. Вероятность повреждения изделия в пути равна $0,002$. Найти закон распределения случайной величины $X$, равной числу поврежденных изделий; чему равно $M\left(X\right),\ D\left(X\right)$.
Пусть дискретная случайная величина $X$ - число поврежденных изделий. Такая случайная величина подчинена закону распределения Пуассона с параметром $\lambda =np=500\cdot 0,002=1$. Вероятности значений равны $P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$. Очевидно, что все вероятности всех значений $X=0,\ 1,\ \dots ,\ 500$ перечислить невозможно, поэтому мы ограничимся лишь первыми несколькими значениями.
$P\left(X=0\right)={{1^0}\over {0!}}\cdot e^{-1}=0,368;$
$P\left(X=1\right)={{1^1}\over {1!}}\cdot e^{-1}=0,368;$
$P\left(X=2\right)={{1^2}\over {2!}}\cdot e^{-1}=0,184;$
$P\left(X=3\right)={{1^3}\over {3!}}\cdot e^{-1}=0,061;$
$P\left(X=4\right)={{1^4}\over {4!}}\cdot e^{-1}=0,015;$
$P\left(X=5\right)={{1^5}\over {5!}}\cdot e^{-1}=0,003;$
$P\left(X=6\right)={{1^6}\over {6!}}\cdot e^{-1}=0,001;$
$P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$
Закон распределения случайной величины $X$:
$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & ... & k \\
\hline
P_i & 0,368; & 0,368 & 0,184 & 0,061 & 0,015 & 0,003 & 0,001 & ... & {{{\lambda }^k}\over {k!}}\cdot e^{-\lambda } \\
\hline
\end{array}$
Для такой случайной величины математическое ожидание и дисперсия равным между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda =1$.
3. Геометрический закон распределения.
Если дискретная случайная величина $X$ может принимать только натуральные значения $1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=p{\left(1-p\right)}^{k-1},\ k=1,\ 2,\ 3,\ \dots $, то говорят, что такая случайная величина $X$ подчинена геометрическому закону распределения вероятностей. Фактически, геометрическое распределения представляется собой испытания Бернулли до первого успеха.
Пример . Примерами случайных величин, имеющих геометрическое распределение, могут быть: число выстрелов до первого попадания в цель; число испытаний прибора до первого отказа; число бросаний монеты до первого выпадения орла и т.д.
Математическое ожидание и дисперсия случайной величины, подчиненной геометрическому распределению, соответственно равны $M\left(X\right)=1/p$, $D\left(X\right)=\left(1-p\right)/p^2$.
Пример . На пути движения рыбы к месту нереста находится $4$ шлюза. Вероятность прохода рыбы через каждый шлюз $p=3/5$. Построить ряд распределения случайной величины $X$ - число шлюзов, пройденных рыбой до первого задержания у шлюза. Найти $M\left(X\right),\ D\left(X\right),\ \sigma \left(X\right)$.
Пусть случайная величина $X$ - число шлюзов, пройденных рыбой до первого задержания у шлюза. Такая случайная величина подчинена геометрическому закону распределения вероятностей. Значения, которые может принимать случайная величина $X:$ 1, 2, 3, 4. Вероятности этих значений вычисляются по формуле: $P\left(X=k\right)=pq^{k-1}$, где: $p=2/5$ - вероятность задержания рыбы через шлюз, $q=1-p=3/5$ - вероятность прохода рыбы через шлюз, $k=1,\ 2,\ 3,\ 4$.
$P\left(X=1\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^0={{2}\over {5}}=0,4;$
$P\left(X=2\right)={{2}\over {5}}\cdot {{3}\over {5}}={{6}\over {25}}=0,24;$
$P\left(X=3\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^2={{2}\over {5}}\cdot {{9}\over {25}}={{18}\over {125}}=0,144;$
$P\left(X=4\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^3+{\left({{3}\over {5}}\right)}^4={{27}\over {125}}=0,216.$
$\begin{array}{|c|c|}
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\left(X_i\right) & 0,4 & 0,24 & 0,144 & 0,216 \\
\hline
\end{array}$
Математическое ожидание:
$M\left(X\right)=\sum^n_{i=1}{x_ip_i}=1\cdot 0,4+2\cdot 0,24+3\cdot 0,144+4\cdot 0,216=2,176.$
Дисперсия:
$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2=}0,4\cdot {\left(1-2,176\right)}^2+0,24\cdot {\left(2-2,176\right)}^2+0,144\cdot {\left(3-2,176\right)}^2+$
$+\ 0,216\cdot {\left(4-2,176\right)}^2\approx 1,377.$
Среднее квадратическое отклонение:
$\sigma \left(X\right)=\sqrt{D\left(X\right)}=\sqrt{1,377}\approx 1,173.$
4. Гипергеометрический закон распределения.
Если $N$ объектов, среди которых $m$ объектов обладают заданным свойством. Случайных образом без возвращения извлекают $n$ объектов, среди которых оказалось $k$ объектов, обладающих заданным свойством. Гипергеометрическое распределение дает возможность оценить вероятность того, что ровно $k$ объектов в выборке обладают заданным свойством. Пусть случайная величина $X$ - число объектов в выборке, обладающих заданным свойством. Тогда вероятности значений случайной величины $X$:
$P\left(X=k\right)={{C^k_mC^{n-k}_{N-m}}\over {C^n_N}}$
Замечание . Статистическая функция ГИПЕРГЕОМЕТ мастера функций $f_x$ пакета Excel дает возможность определить вероятность того, что определенное количество испытаний будет успешным.
$f_x\to $ статистические $\to $ ГИПЕРГЕОМЕТ $\to $ ОК . Появится диалоговое окно, которое нужно заполнить. В графе Число_успехов_в_выборке указываем значение $k$. Размер_выборки равен $n$. В графе Число_успехов_в_совокупности указываем значение $m$. Размер_совокупности равен $N$.
Математическое ожидание и дисперсия дискретной случайной величины $X$, подчиненной геометрическому закону распределения, соответственно равны $M\left(X\right)=nm/N$, $D\left(X\right)={{nm\left(1-{{m}\over {N}}\right)\left(1-{{n}\over {N}}\right)}\over {N-1}}$.
Пример . В кредитном отделе банка работают 5 специалистов с высшим финансовым образованием и 3 специалиста с высшим юридическим образованием. Руководство банка решило направить 3 специалистов Для повышения квалификации, отбирая их в случайном порядке.
а) Составьте ряд распределения числа специалистов с высшим финансовым образованием, которые могут быть направлены на повышение квалификации;
б) Найдите числовые характеристики этого распределения.
Пусть случайная величина $X$ - число специалистов с высшим финансовым образованием среди трех отобранных. Значения, которые может принимать $X:0,\ 1,\ 2,\ 3$. Данная случайная величина $X$ распределена по гипергеометрическому распределению с параметрами: $N=8$ - размер совокупности, $m=5$ - число успехов в совокупности, $n=3$ - размер выборки, $k=0,\ 1,\ 2,\ 3$ - число успехов в выборке. Тогда вероятности $P\left(X=k\right)$ можно рассчитать по формуле: $P(X=k)={C_{m}^{k} \cdot C_{N-m}^{n-k} \over C_{N}^{n} } $. Имеем:
$P\left(X=0\right)={{C^0_5\cdot C^3_3}\over {C^3_8}}={{1}\over {56}}\approx 0,018;$
$P\left(X=1\right)={{C^1_5\cdot C^2_3}\over {C^3_8}}={{15}\over {56}}\approx 0,268;$
$P\left(X=2\right)={{C^2_5\cdot C^1_3}\over {C^3_8}}={{15}\over {28}}\approx 0,536;$
$P\left(X=3\right)={{C^3_5\cdot C^0_3}\over {C^3_8}}={{5}\over {28}}\approx 0,179.$
Тогда ряд распределения случайной величины $X$:
$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0,018 & 0,268 & 0,536 & 0,179 \\
\hline
\end{array}$
Рассчитаем числовые характеристики случайной величины $X$ по общим формулам гипергеометрического распределения.
$M\left(X\right)={{nm}\over {N}}={{3\cdot 5}\over {8}}={{15}\over {8}}=1,875.$
$D\left(X\right)={{nm\left(1-{{m}\over {N}}\right)\left(1-{{n}\over {N}}\right)}\over {N-1}}={{3\cdot 5\cdot \left(1-{{5}\over {8}}\right)\cdot \left(1-{{3}\over {8}}\right)}\over {8-1}}={{225}\over {448}}\approx 0,502.$
$\sigma \left(X\right)=\sqrt{D\left(X\right)}=\sqrt{0,502}\approx 0,7085.$
Глава 7.
Конкретные законы распределения случайных величин
Виды законов распределения дискретных случайных величин
Пусть дискретная случайная величина может принимать значения х 1 , х 2 , …, х n , … . Вероятности этих значений могут быть вычислены по различным формулам, например, при помощи основных теорем теории вероятностей, формулы Бернулли или по каким-то другим формулам. Для некоторых из этих формул закон распределения имеет свое название.
Наиболее часто встречающимися законами распределения дискретной случайной величины являются биномиальный, геометрический, гипергеометрический, закон распределения Пуассона.
Биномиальный закон распределения
Пусть производится n независимых испытаний, в каждом из которых может появиться или не появиться событие А . Вероятность появления этого события в каждом единичном испытании постоянна, не зависит от номера испытания и равна р =Р (А ). Отсюда вероятность не появления события А в каждом испытании также постоянна и равна q =1–р . Рассмотрим случайную величину Х равную числу появлений события А в n испытаниях. Очевидно, что значения этой величины равны
х 1 =0 – событие А в n испытаниях не появилось;
х 2 =1 – событие А в n испытаниях появилось один раз;
х 3 =2 – событие А в n испытаниях появилось два раза;
…………………………………………………………..
х n +1 = n – событие А в n испытаниях появилось все n раз.
Вероятности этих значений могут быть вычислены по формуле Бернулли (4.1):
где к =0, 1, 2, …, n .
Биномиальным законом распределения Х , равной числу успехов в n испытаниях Бернулли, с вероятностью успеха р .
Итак, дискретная случайная величина имеет биномиальное распределение (или распределена по биномиальному закону), если ее возможные значения 0, 1, 2, …, n , а соответствующие вероятности вычисляются по формуле (7.1).
Биномиальное распределение зависит от двух параметров р и n .
Ряд распределения случайной величины, распределенной по биномиальному закону, имеет вид:
| Х | … | k | … | n | ||
| Р | | … | … | |
Пример 7.1 . Производится три независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,4. Случайная величина Х – число попаданий в мишень. Построить ее ряд распределения.
Решение. Возможными значениями случайной величины Х являются х 1 =0; х 2 =1; х 3 =2; х 4 =3. Найдем соответствующие вероятности, используя формулу Бернулли. Нетрудно показать, что применение этой формулы здесь вполне оправдано. Отметим, что вероятность не попадания в цель при одном выстреле будет равна 1-0,4=0,6. Получим

Ряд распределения имеет следующий вид:
| Х | ||||
| Р | 0,216 | 0,432 | 0,288 | 0,064 |
Нетрудно проверить, что сумма всех вероятностей равна 1. Сама случайная величина Х распределена по биномиальному закону. ■
Найдем математическое ожидание и дисперсию случайной величины, распределенной по биномиальному закону.
При решении примера 6.5 было показано, что математическое ожидание числа появлений события А в n независимых испытаниях, если вероятность появления А в каждом испытании постоянна и равна р , равно n ·р
В этом примере использовалась случайная величина, распределенная по биномиальному закону. Поэтому решение примера 6.5, по сути является доказательством следующей теоремы.
Теорема 7.1. Математическое ожидание дискретной случайной величины, распределенной по биномиальному закону, равно произведению числа испытаний на вероятность "успеха", т.е. М (Х )= n ·р.
Теорема 7.2. Дисперсия дискретной случайной величины, распределенной по биномиальному закону, равна произведению числа испытаний на вероятность "успеха" и на вероятность "неудачи", т.е. D (Х )= nрq.
Асимметрия и эксцесс случайной величины, распределенной по биномиальному закону, определяются по формулам
Эти формулы можно получить, воспользовавшись понятием начальных и центральных моментов.
Биномиальный закон распределения лежит в основе многих реальных ситуаций. При больших значениях n биномиальное распределение может быть аппроксимировано с помощью других распределений, в частности с помощью распределения Пуассона.
Распределение Пуассона
Пусть имеется n испытаний Бернулли, при этом число испытаний n достаточно велико. Ранее было показано, что в этом случае (если к тому же вероятность р события А очень мала) для нахождения вероятности того, что событие А появиться т раз в испытаниях можно воспользоваться формулой Пуассона (4.9). Если случайная величина Х означает число появлений события А в n испытаниях Бернулли, то вероятность того, что Х примет значение k может быть вычислена по формуле
 , (7.2)
, (7.2)
где λ = nр .
Законом распределения Пуассона называется распределение дискретной случайной величины Х , для которой возможными значениями являются целые неотрицательные числа, а вероятности р т этих значений находятся по формуле (7.2).
Величина λ = nр называется параметром распределения Пуассона.
Случайная величина, распределенная по закону Пуассона, может принимать бесконечное множество значений. Так как для этого распределения вероятность р появления события в каждом испытании мала, то это распределение иногда называют законом редких явлений.
Ряд распределения случайной величины, распределенной по закону Пуассона, имеет вид
| Х | … | т | … | ||||
| Р | … | … |
Нетрудно убедиться, что сумма вероятностей второй строки равна 1. Для этого необходимо вспомнить, что функцию можно разложить в ряд Маклорена, который сходится для любого х . В данном случае имеем
 . (7.3)
. (7.3)
Как было отмечено, закон Пуассона в определенных предельных случаях заменяет биномиальный закон. В качестве примера можно привести случайную величину Х , значения которой равны количеству сбоев за определенный промежуток времени при многократном применении технического устройства. При этом предполагается, что это устройство высокой надежности, т.е. вероятность сбоя при одном применении очень мала.
Кроме таких предельных случаев, на практике встречаются случайные величины, распределенные по закону Пуассона, не связанные с биномиальным распределением. Например, распределение Пуассона часто используется тогда, когда имеют дело с числом событий, появляющихся в промежутке времени (число поступлений вызовов на телефонную станцию в течение часа, число машин, прибывших на авто мойку в течение суток, число остановок станков в неделю и т.п.). Все эти события должны образовывать, так называемый поток событий, который является одним из основных понятий теории массового обслуживания. Параметр λ характеризует среднюю интенсивность потока событий.
Пример 7.2 . На факультете насчитывается 500 студентов. Какова вероятность того, что 1 сентября является днем рождения для трех студентов данного факультета?
Решение . Так как число студентов n =500 достаточно велико и р – вероятность родится первого сентября любому из студентов равна , т.е. достаточно мала, то можно считать, что случайная величина Х – число студентов, родившихся первого сентября, распределена по закону Пуассона с параметром λ = np = =1,36986. Тогда, по формуле (7.2) получим
Теорема 7.3. Пусть случайная величинаХ распределена по закону Пуассона. Тогда ее математическое ожидание и дисперсия равны друг другу и равны значению параметра λ , т.е. M (X ) = D (X ) = λ = np .
Доказательство. По определению математического ожидания, используя формулу (7.3) и ряд распределения случайной величины, распределенной по закону Пуассона, получим
Прежде, чем найти дисперсию, найдем вначале математическое ожидание квадрата рассматриваемой случайной величины. Получаем

Отсюда, по определению дисперсии, получаем
Теорема доказана.
Применяя понятия начальных и центральных моментов, можно показать, что для случайной величины, распределенной по закону Пуассона, коэффициенты асимметрии и эксцесса определяются по формулам
Нетрудно понять, что, так как по смысловому содержанию параметр λ = np положителен, то у случайной величины, распределенной по закону Пуассона, всегда положительны и асимметрия и эксцесс.
Приветствую всех читателей!
Статистический анализ, как известно, занимается сбором и обработкой реальных данных. Дело полезное, а зачастую и выгодное, т.к. правильные выводы позволяют избежать ошибок и потерь в будущем, а иногда и правильно угадать это самое будущее. Собранные данные отражают состояние некоторого наблюдаемого явления. Данные часто (но не всегда) имеют числовой вид и с ними можно проделывать различные математические манипуляции, извлекая тем самым дополнительную информацию.
Однако не все явления измеряются в количественной шкале типа 1, 2, 3 … 100500 … Не всегда явление может принимать бесконечное или большое количество различных состояний. Например, пол у человека может быть либо М, либо Ж. Стрелок либо попадает в цель, либо не попадает. Голосовать можно либо «За», либо «Против» и т.д. и т.п. Другими словами, такие данные отражают состояние альтернативного признака – либо «да» (событие наступило), либо «нет» (событие не наступило). Наступившее событие (положительный исход) еще называют «успехом». Такие явления также могут носить массовый и случайный характер. Следовательно, их можно измерять и делать статистически обоснованные выводы.
Эксперименты с такими данными называются схемой Бернулли , в честь известного швейцарского математика, который установил, что при большом количестве испытаний соотношение положительных исходов и общего количества испытаний стремится к вероятности наступления этого события.
Переменная альтернативного признака
Для того, чтобы в анализе задействовать математический аппарат, результаты подобных наблюдений следует записать в числовом виде. Для этого положительному исходу присваивают число 1, отрицательному – 0. Другими словами, мы имеем дело с переменной, которая может принимать только два значения: 0 или 1.
Какую пользу отсюда можно извлечь? Вообще-то не меньшую, чем от обычных данных. Так, легко подсчитать количество положительных исходов – достаточно просуммировать все значения, т.е. все 1 (успехи). Можно пойти далее, но для этого потребуется ввести парочку обозначений.
Первым делом нужно отметить, что положительные исходы (которые равны 1) имеют некоторую вероятность появления. Например, выпадение орла при подбрасывании монеты равно ½ или 0,5. Такая вероятность традиционно обозначается латинской буквой p . Следовательно, вероятность наступления альтернативного события равна 1 — p , которую еще обозначают через q , то есть q = 1 – p . Указанные обозначения можно наглядно систематизировать в виде таблички распределения переменной X .
Теперь у нас есть перечень возможных значений и их вероятности. Можно приступить к расчету таких замечательных характеристик случайной величины, как математическое ожидание и дисперсия . Напомню, что математическое ожидание рассчитывается, как сумма произведений всех возможных значений на соответствующие им вероятности:
![]()
Вычислим матожидание, используя обозначения в таблицы выше.
Получается, что математическое ожидание альтернативного признака равно вероятности этого события – p .
Теперь определим, что такое дисперсия альтернативного признака. Также напомню, что дисперсия – есть средний квадрат отклонений от математического ожидания. Общая формула (для дискретных данных) имеет вид:
Отсюда дисперсия альтернативного признака:

Нетрудно заметить, что эта дисперсия имеет максимум 0,25 (при p=0,5) .
Среднее квадратическое отклонение – корень из дисперсии:
Максимальное значение не превышает 0,5.
Как видно, и математическое ожидание, и дисперсия альтернативного признака имеют очень компактный вид.
Биномиальное распределение случайной величины
Теперь рассмотрим ситуацию под другим углом. Действительно, кому интересно, что среднее выпадение орлов при одном бросании равно 0,5? Это даже невозможно представить. Интересней поставить вопрос о числе выпадения орлов при заданном количестве подбрасываний.
Другими словами, исследователя часто интересует вероятность наступления некоторого числа успешных событий. Это может быть количество бракованных изделий в проверяемой партии (1- бракованная, 0 — годная) или количество выздоровлений (1 – здоров, 0 – больной) и т.д. Количество таких «успехов» будет равно сумме всех значений переменной X , т.е. количеству единичных исходов.
Случайная величина B называется биномиальной и принимает значения от 0 до n (при B = 0 — все детали годные, при B = n – все детали бракованные). Предполагается, что все значения x независимы между собой. Рассмотрим основные характеристики биномиальной переменной, то есть установим ее математическое ожидание, дисперсию и распределение.
Матожидание биномиальной переменной получить очень легко. Вспомним, что есть сумма математических ожиданий каждой складываемой величины, а оно у всех одинаковое, поэтому:
Например, математическое ожидание количества выпавших орлов при 100 подбрасываниях равно 100 × 0,5 = 50.
Теперь выведем формулу дисперсии биномиальной переменной. есть сумма дисперсий. Отсюда
Среднее квадратическое отклонение, соответственно
Для 100 подбрасываний монеты среднеквадратическое отклонение равно
И, наконец, рассмотрим распределение биномиальной величины, т.е. вероятности того, что случайная величина B будет принимать различные значения k , где 0≤ k ≤n . Для монеты эта задача может звучать так: какова вероятность выпадения 40 орлов при 100 бросках?
Чтобы понять метод расчета, представим, что монета подбрасывается всего 4 раза. Каждый раз может выпасть любая из сторон. Мы задаемся вопросом: какова вероятность выпадения 2 орлов из 4 бросков. Каждый бросок независим друг от друга. Значит, вероятность выпадения какой-либо комбинации будет равна произведению вероятностей заданного исхода для каждого отдельного броска. Пусть О – это орел, Р – решка. Тогда, к примеру, одна из устраивающих нас комбинаций может выглядеть как ООРР, то есть:

Вероятность такой комбинации равняется произведению двух вероятностей выпадения орла и еще двух вероятностей не выпадения орла (обратное событие, рассчитываемое как 1 — p ), т.е. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Такова вероятность одной из устраивающих нас комбинации. Но вопрос ведь стоял об общем количестве орлов, а не о каком-то определенном порядке. Тогда нужно сложить вероятности всех комбинаций, в которых присутствует ровно 2 орла. Ясно, все они одинаковы (от перемены мест множителей произведение не меняется). Поэтому нужно вычислить их количество, а затем умножить на вероятность любой такой комбинации. Подсчитаем все варианты сочетаний из 4 бросков по 2 орла: РРОО, РОРО, РООР, ОРРО, ОРОР, ООРР. Всего 6 вариантов.

Следовательно, искомая вероятность выпадения 2 орлов после 4 бросков равна 6×0,0625=0,375.
Однако подсчет подобным образом утомителен. Уже для 10 монет методом перебора получить общее количество вариантов будет очень трудно. Поэтому умные люди давно изобрели формулу, с помощью которой рассчитывают количество различных сочетаний из n элементов по k , где n – общее количество элементов, k – количество элементов, варианты расположения которых и подсчитываются. Формула сочетания из n элементов по k такова:
![]()
Подобные вещи проходят в разделе комбинаторики. Всех желающих подтянуть знания отправляю туда. Отсюда, кстати, и название биномиального распределения (формула выше является коэффициентом в разложении бинома Ньютона).
Формулу для определения вероятности легко обобщить на любое количество n и k . В итоге формула биномиального распределения имеет следующий вид.
Словами: количество подходящих под условие комбинаций умножить на вероятность одной из них.
Для практического использования достаточно просто знать формулу биномиального распределения. А можно даже и не знать – ниже показано, как определить вероятность с помощью Excel. Но лучше все-таки знать.
Рассчитаем по этой формуле вероятность выпадения 40 орлов при 100 бросках:
Или всего 1,08%. Для сравнения вероятность наступления математического ожидания этого эксперимента, то есть 50 орлов, равна 7,96%. Максимальная вероятность биномиальной величины принадлежит значению, соответствующему математическому ожиданию.
Расчет вероятностей биномиального распределения в Excel
Если использовать только бумагу и калькулятор, то расчеты по формуле биноминального распределения, несмотря на отсутствие интегралов, даются довольно тяжело. К примеру значение 100! – имеет более 150 знаков. Вручную рассчитать такое невозможно. Раньше, да и сейчас тоже, для вычисления подобных величин использовали приближенные формулы. В настоящий момент целесообразно использовать специальное ПО, типа MS Excel. Таким образом, любой пользователь (даже гуманитарий по образованию) вполне может вычислить вероятность значения биномиально распределенной случайной величины.
Для закрепления материала задействуем Excel пока в качестве обычного калькулятора, т.е. произведем поэтапное вычисление по формуле биномиального распределения. Рассчитаем, например, вероятность выпадения 50 орлов. Ниже приведена картинка с этапами вычислений и конечным результатом.

Как видно, промежуточные результаты имеют такой масштаб, что не помещаются в ячейку, хотя везде и используются простые функции типа: ФАКТР (вычисление факториала), СТЕПЕНЬ (возведение числа в степень), а также операторы умножения и деления. Более того, этот расчет довольно громоздок, во всяком случаен не является компактным, т.к. задействовано много ячеек. Да и разобраться с ходу трудновато.
В общем в Excel предусмотрена готовая функция для вычисления вероятностей биномиального распределения. Функция называется БИНОМ.РАСП.

Число успехов – количество успешных испытаний. У нас их 50.
Число испытаний – количество подбрасываний: 100 раз.
Вероятность успеха – вероятность выпадения орла при одном подбрасывании 0,5.
Интегральная – указывается либо 1, либо 0. Если 0, то рассчитается вероятность P(B=k) ; если 1, то рассчитается функция биномиального распределения, т.е. сумма всех вероятностей от B=0 до B=k включительно.
Нажимаем ОК и получаем тот же результат, что и выше, только все рассчиталось одной функцией.

Очень удобно. Эксперимента ради вместо последнего параметра 0 поставим 1. Получим 0,5398. Это значит, что при 100 подкидываниях монеты вероятность выпадения орлов в количестве от 0 до 50 равна почти 54%. А поначалу то казалось, что должно быть 50%. В общем, расчеты производятся легко и быстро.
Настоящий аналитик должен понимать, как ведет себя функция (каково ее распределение), поэтому произведем расчет вероятностей для всех значений от 0 до 100. То есть зададимся вопросом: какова вероятность, что не выпадет ни одного орла, что выпадет 1 орел, 2, 3, 50, 90 или 100. Расчет приведен в нижеследующей самодвигающейся картинке. Синяя линия – само биномиальное распределение, красная точка – вероятность для конкретного числа успехов k.

Кто-то может спросить, а не похоже ли биномиальное распределение на… Да, очень похоже. Еще Муавр (в 1733 г.) говорил, что биномиальное распределение при больших выборках приближается к (не знаю, как это тогда называлось), но его никто не слушал. Только Гаусс, а затем и Лаплас через 60-70 лет вновь открыли и тщательно изучили нормальной закон распределения. На графике выше отлично видно, что максимальная вероятность приходится на математическое ожидание, а по мере отклонения от него, резко снижается. Также, как и у нормального закона.
Биномиальное распределение имеет большое практическое значение, встречается довольно часто. С помощью Excel расчеты проводятся легко и быстро. Так что можно смело использовать.
На этом предлагаю распрощаться до следующей встречи. Всех благ, будьте здоровы!
Биномиальное распределение - одно из важнейших распределений вероятностей дискретно изменяющейся случайной величины. Биномиальным распределением называется распределение вероятностей числа m наступления события А в n взаимно независимых наблюдениях . Часто событие А называют "успехом" наблюдения, а противоположное ему событие - "неуспехом", но это обозначение весьма условное.
Условия биномиального распределения :
- в общей сложности проведено n испытаний, в которых событие А может наступить или не наступить;
- событие А в каждом из испытаний может наступить с одной и той же вероятностью p ;
- испытания являются взаимно независимыми.
Вероятность того, что в n испытаниях событие А наступит именно m раз, можно вычислить по формуле Бернулли:
![]()
![]() ,
,
где p - вероятность наступления события А ;
q = 1 - p - вероятность наступления противоположного события .
Разберёмся, почему биномиальное распределение описанным выше образом связано с формулой Бернулли . Событие - число успехов при n испытаниях распадается на ряд вариантов, в каждом из которых успех достигается в m испытаниях, а неуспех - в n - m испытаниях. Рассмотрим один из таких вариантов - B 1 . По правилу сложения вероятностей умножаем вероятности противоположных событий:
![]() ,
,
а если обозначим q = 1 - p , то
![]() .
.
Такую же вероятность будет иметь любой другой вариант, в котором m успехов и n - m неуспехов. Число таких вариантов равно - числу способов, которыми можно из n испытаний получить m успехов.
Сумма вероятностей всех m чисел наступления события А (чисел от 0 до n ) равна единице:
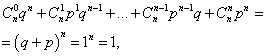
где каждое слагаемое представляет собой слагаемое бинома Ньютона. Поэтому рассматриваемое распределение и называется биномиальным распределением.
На практике часто необходимо вычислять вероятности "не более m успехов в n испытаниях" или "не менее m успехов в n испытаниях". Для этого используются следующие формулы.
Интегральную функцию, то есть вероятность F (m ) того, что в n наблюдениях событие А наступит не более m раз , можно вычислить по формуле:
В свою очередь вероятность F (≥m ) того, что в n наблюдениях событие А наступит не менее m раз , вычисляется по формуле:
Иногда бывает удобнее вычислять вероятность того, что в n наблюдениях событие А наступит не более m раз, через вероятность противоположного события:
![]() .
.
Какой из формул пользоваться, зависит от того, в какой из них сумма содержит меньше слагаемых.
Характеристики биномиального распределения вычисляются по следующим формулам .
Математическое ожидание: .
Дисперсия: .
Среднеквадратичное отклонение: .
Биномиальное распределение и расчёты в MS Excel
Вероятность биномиального распределения P n (m ) и значения интегральной функции F (m ) можно вычислить при помощи функции MS Excel БИНОМ.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).

MS Excel требует ввести следующие данные:
- число успехов;
- число испытаний;
- вероятность успеха;
- интегральная - логическое значение: 0 - если нужно вычислить вероятность P n (m ) и 1 - если вероятность F (m ).
Пример 1. Менеджер фирмы обобщил информацию о числе проданных в течение последних 100 дней фотокамер. В таблице обобщена информация и рассчитаны вероятности того, что в день будет продано определённое число фотокамер.
День завершён с прибылью, если продано 13 или более фотокамер. Вероятность, что день будет отработан с прибылью:
![]()
Вероятность того, что день будет отработан без прибыли:

Пусть вероятность того, что день отработан с прибылью, является постоянной и равна 0,61, и число проданных в день фотокамер не зависит от дня. Тогда можно использовать биномиальное распределение, где событие А - день будет отработан с прибылью, - без прибыли.
Вероятность того, что из 6 дней все будут отработаны с прибылью:
![]() .
.
Тот же результат получим, используя функцию MS Excel БИНОМ.РАСП (значение интегральной величины - 0):
P 6 (6 ) = БИНОМ.РАСП(6; 6; 0,61; 0) = 0,052.
Вероятность того, что из 6 дней 4 и больше дней будут отработаны с прибылью:
где ![]() ,
,
![]() ,
,
Используя функцию MS Excel БИНОМ.РАСП, вычислим вероятность того, что из 6 дней не более 3 дней будут завершены с прибылью (значение интегральной величины - 1):
P 6 (≤3 ) = БИНОМ.РАСП(3; 6; 0,61; 1) = 0,435.
Вероятность того, что из 6 дней все будут отработаны с убытками:
![]() ,
,
Тот же показатель вычислим, используя функцию MS Excel БИНОМ.РАСП:
P 6 (0 ) = БИНОМ.РАСП(0; 6; 0,61; 0) = 0,0035.
Решить задачу самостоятельно, а затем посмотреть решение
Пример 2. В урне 2 белых шара и 3 чёрных. Из урны вынимают шар, устанавливают цвет и кладут обратно. Попытку повторяют 5 раз. Число появления белых шаров - дискретная случайная величина X , распределённая по биномиальному закону. Составить закон распределения случайной величины. Определить моду, математическое ожидание и дисперсию.
Продолжаем решать задачи вместе
Пример 3. Из курьерской службы отправились на объекты n = 5 курьеров. Каждый курьер с вероятностью p = 0,3 независимо от других опаздывает на объект. Дискретная случайная величина X - число опоздавших курьеров. Построить ряд распределения это случайной величины. Найти её математическое ожидание, дисперсию, среднее квадратическое отклонение. Найти вероятность того, что на объекты опоздают не менее двух курьеров.




